Advertisements
Advertisements
प्रश्न
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
उत्तर
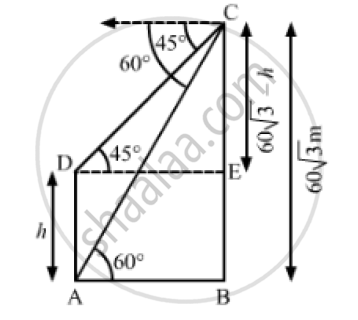
Let AD be the tower and BC be the cliff.
We have,
BC = 60 `sqrt(3)` , ∠ CDE = 45° and ∠BAC = 60°
Let AD = h
⇒ BE = AD = h
⇒ CE = BC - BE= 60 `sqrt(3)` - h
In ΔCDE,
` tan 45° = (CE)/(DE)`
`⇒ 1 = (60 sqrt(3) -h)/(DE)`
`⇒ DE = 60 sqrt(3) - h`
`⇒ AB = DE = 60 sqrt(3) - h` ............(1)
Now, in ΔABC
`tan 60° = (BC)/(AB)`
`⇒ sqrt(3)= (60 sqrt(3) )/ (60 sqrt(3) -h)` [ Using (1)]
`⇒ 180 - h sqrt(3) = 60 sqrt(3)`
`⇒ h sqrt(3) = 180- 60 sqrt(3)`
`⇒ h = (108 -60sqrt(3) )/sqrt(3) xx sqrt(3)/sqrt(3)`
`⇒ h = ( 180 sqrt(3)-180) /3`
`⇒ h = (180 sqrt(3)-1) /3`
∴` h = 60 ( sqrt(3)-1)`
= 60 (1.732 -1)
= 60 (0.7.32)
Also, h = 43.92m
So, the height of the tower is 43. 92 m.
संबंधित प्रश्न
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Find the speed of flying of the bird.
`("Take"sqrt3=1.732)`
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
