Advertisements
Advertisements
प्रश्न
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
उत्तर
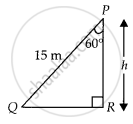
Given that, the height of the ladder = 15 m
Let the height of the vertical wall = h
And the ladder makes an angle of elevation 60° with the wall i.e., θ = 60°
In ΔQPR,
cos 60° = `"PR"/"PQ" = "h"/15`
⇒ `1/2 = "h"/15`
⇒ h = `15/2`m
Hence, the required height of the wall `15/2`m.
APPEARS IN
संबंधित प्रश्न
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground form the just observation point.
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
A tower subtends an angle 𝛼 at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tan α cot β
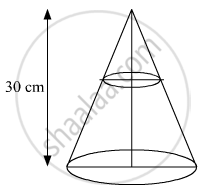
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
A tower stands vertically on the ground. From a point on the ground, which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
