Advertisements
Advertisements
प्रश्न
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
उत्तर
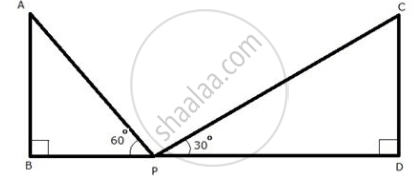
Let AB and CD be the two towers of length 'l' m.
Let P be a point in the roadway BD such that BD = 100 m, ∠APB = 60° and ∠CPD = 30°
In ΔABP,
`"AB"/"BP" = tan 60^circ`
`=> "BP" = "l"/(tan 60^circ)`
`=> "BP" = "l"/sqrt3`
In ΔCDP,
`"CD"/"DP" = tan 30^circ`
`=> "CD"/"DP" = 1/sqrt3`
`=> "l"/"DP" = 1/sqrt3`
`=> "DP" = "l" sqrt3`
`=> "DP" = "l" sqrt3`
The total width of the road is the sum of BP and PD:
∴ BP + PD = 100
∴ `l/sqrt3 + l sqrt3 = 100`
∴ `l (1/sqrt3 + sqrt3) = 100`
∴ `l (1/1.732 + 1.732) = 100` ...[Given `sqrt3` = 1.732]
∴ `l ((1 + 1.732 xx 1.732)/1.732) = 100`
∴ `l( (1 + 2.9998)/1.732) = 100`
∴ `l( (3.9998)/1.732) = 100`
∴ `100/2.309 = l`
∴ l = 43.31 m approx.
Hence, length of the piller is 43.31 m
The point is BP = `l/sqrt3`
The length of the pillars (l) and the position of point P (BP).
∴ BP = `l/sqrt3`
∴ BP = `43.31/1.732`
∴ BP = 25.00 meters.
The length of the pillars (l) and the position of point P (PD).
∴ `"DP" = "l" sqrt3`
∴ DP = 43.31 × 1.732
∴ DP = 75.01 meters.
The distance from the first pillar (associated with the 60° angle of elevation) to point P is approximately 25.00 meters.
The distance from the second pillar (associated with the 30° angle of elevation) to point P is approximately 75.01 meters.
APPEARS IN
संबंधित प्रश्न
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
A fire in a building B is reported on the telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel?
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
