Advertisements
Advertisements
प्रश्न
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
उत्तर
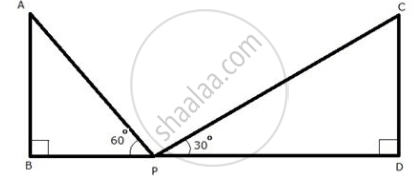
Let AB and CD be the two towers of length 'l' m.
Let P be a point in the roadway BD such that BD = 100 m, ∠APB = 60° and ∠CPD = 30°
In ΔABP,
`"AB"/"BP" = tan 60^circ`
`=> "BP" = "l"/(tan 60^circ)`
`=> "BP" = "l"/sqrt3`
In ΔCDP,
`"CD"/"DP" = tan 30^circ`
`=> "CD"/"DP" = 1/sqrt3`
`=> "l"/"DP" = 1/sqrt3`
`=> "DP" = "l" sqrt3`
`=> "DP" = "l" sqrt3`
The total width of the road is the sum of BP and PD:
∴ BP + PD = 100
∴ `l/sqrt3 + l sqrt3 = 100`
∴ `l (1/sqrt3 + sqrt3) = 100`
∴ `l (1/1.732 + 1.732) = 100` ...[Given `sqrt3` = 1.732]
∴ `l ((1 + 1.732 xx 1.732)/1.732) = 100`
∴ `l( (1 + 2.9998)/1.732) = 100`
∴ `l( (3.9998)/1.732) = 100`
∴ `100/2.309 = l`
∴ l = 43.31 m approx.
Hence, length of the piller is 43.31 m
The point is BP = `l/sqrt3`
The length of the pillars (l) and the position of point P (BP).
∴ BP = `l/sqrt3`
∴ BP = `43.31/1.732`
∴ BP = 25.00 meters.
The length of the pillars (l) and the position of point P (PD).
∴ `"DP" = "l" sqrt3`
∴ DP = 43.31 × 1.732
∴ DP = 75.01 meters.
The distance from the first pillar (associated with the 60° angle of elevation) to point P is approximately 25.00 meters.
The distance from the second pillar (associated with the 30° angle of elevation) to point P is approximately 75.01 meters.
APPEARS IN
संबंधित प्रश्न
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by `\text{cot }\theta =\frac{bcot alpha -a\cot \beta }{b-a}`
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Find the angle of elevation of the sun when the shadow of a pole h metres high is `sqrt(3)` h metres long.
