Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
विकल्प
\[50\sqrt{3}\]
50
\[\frac{50}{\sqrt{2}}\]
\[\frac{50}{\sqrt{3}}\]
उत्तर
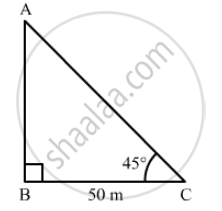
Suppose AB is the tower and C is a point on the ground.
It is given that, BC = 50 m and \[\angle\]ACB = 45°.
In right ∆ABC,
\[\tan45°= \frac{AB}{BC}\]
\[ \Rightarrow 1 = \frac{AB}{50}\]
\[ \Rightarrow AB = 50 m\]
Thus, the height of the tower is 50 m.
APPEARS IN
संबंधित प्रश्न
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
A kite is flying at a height of 30 m from the ground. The length of string from the kite to the ground is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is ____________.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
