Advertisements
Advertisements
प्रश्न
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
उत्तर
Let the height of the electric pole AD be “h” m
EC = 15 – h m
Let AB be “x”
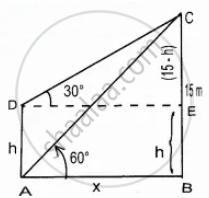
In the right ∆ABC, tan 60° = `"BC"/"AB"`
`sqrt(3) = 15/x`
x = `15/sqrt(3)`
= `(15 xx sqrt(3))/3`
= `5sqrt(3)`
In the right ∆CDE, tan 30° = `"EC"/"DE"`
`1/sqrt(3) = (15 - "h")/x` ...(1)
Substitute the value of x = `5sqrt(3)` in (1)
`1/sqrt(3) = (15 - "h")/(5sqrt(3))`
⇒ `sqrt(3)(15 - "h") = 5sqrt(3)`
(15 – h) = `(5sqrt(3))/sqrt(3)`
⇒ 15 – h = 5
h = 15 – 5 = 10
∴ Height of the electric pole = 10 m
APPEARS IN
संबंधित प्रश्न
Two building are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 40 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
