Advertisements
Advertisements
प्रश्न
From the top of a rock `50sqrt(3)` m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock
उत्तर
Let the distance of the car from the rock is x m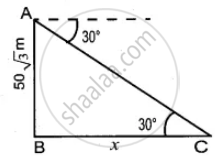
In the right ∆ABC, tan 30° = `"AB"/"BC"`
`1/sqrt(3) = (50sqrt(3))/x`
x = `50sqrt(3) xx sqrt(3)`
= 50 × 3
= 150 m
∴ Distance of the car from the rock = 150 m
APPEARS IN
संबंधित प्रश्न
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
The Distance of the point (−3, 4) from the x-axis is
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
