Advertisements
Advertisements
प्रश्न
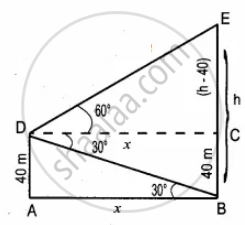
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
उत्तर
Let the height of the hill BE be h m and the distance of the hill from the ship be x m
In the right ∆ABD
tan 30° = `"AD"/"DB"`
`1/sqrt(3) = 40/x`
x = `40sqrt(3)` ...(1)
In the right ∆CDE
tan 60° = `"CE"/"DC"`
`sqrt(3) = ("h" - 40)/x`
x = `("h" - 40)/sqrt(3)` ...(2)
From (1) and (2) we get
`("h" - 40)/sqrt(3) = 40sqrt(3)`
h – 40 = 40 × 3
h = 120 + 40 = 160 m
Height of the hill = 160 m
Distance of the hill from the ship = `40 xx sqrt(3)`
= 40 × 1.732
= 69.28 m
APPEARS IN
संबंधित प्रश्न
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
AB is a pole of height 6 m standing at a point B and CD is a ladder inclined at angle of 600 to the horizontal and reaches upto a point D of pole . If AD = 2.54 m , find the length of the ladder.
If two circles having centers P and Q and radii 3 cm and 5 cm. touch each other externally, find the distance PQ.
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
An observer 2.25 m tall is 42.75 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
Read the following passage:
|
Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure; On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.
|
Based on the above information, answer the following questions:
- Find the length of the wire from the point O to the top of Section B.
- Find the distance AB.
OR
Find the area of ∠OPB. - Find the height of the Section A from the base of the tower.

