Advertisements
Advertisements
प्रश्न
Read the following passage:
|
Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure; On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.
|
Based on the above information, answer the following questions:
- Find the length of the wire from the point O to the top of Section B.
- Find the distance AB.
OR
Find the area of ∠OPB. - Find the height of the Section A from the base of the tower.
उत्तर
i. Let the length of wire BO = x cm
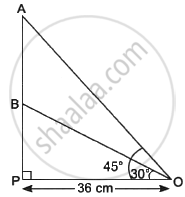
∴ cos 30° = `(PO)/(BO)`
`\implies sqrt(3)/2 = 36/x`
`\implies` x = `(36 xx 2)/sqrt(3) xx sqrt(3)/sqrt(3)`
= `12 xx 2sqrt(3)`
= `24sqrt(3)` cm
ii. In ΔAPO, tan 45° = `(AP)/(PO)`
`\implies` 1 = `(AP)/36`
`\implies` AP = 36 cm ...(1)
Now, In ΔPBO,
tan 30° = `(BP)/(PO)`
`\implies 1/sqrt(3) = (BP)/36`
`\implies` BP = `36/sqrt(3) xx sqrt(3)/sqrt(3)`
= `36/3 sqrt(3)`
= `12sqrt(3)` cm
∴ AB = AP – BP
= `36 - 12sqrt(3)` cm
OR
In ΔOPB
tan 30° = `(BP)/(PO)`
`\implies 1/sqrt(3) = (BP)/36`
BP = `36/sqrt(3)`
= `36/sqrt(3) xx sqrt(3)/sqrt(3)`
= `12sqrt(3)` cm
Now, Area of ΔOPB = `1/2 xx "height" xx "base"`
= `1/2 xx BP xx OP`
= `1/2 xx 12sqrt(3) xx 36`
= `216sqrt(3)` cm2
iii. In ΔAPO, tan 45° = `(AP)/36`
1 = `(AP)/36`
A = 36 cm
Height of section A from the base of the tower = AP = 36 cm
APPEARS IN
संबंधित प्रश्न
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by `\text{cot }\theta =\frac{bcot alpha -a\cot \beta }{b-a}`
A tree is broken by the wind. The top of that tree struck the ground at an angle of 30° and at a distance of 30. Find the height of the whole tree
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ



