Advertisements
Advertisements
प्रश्न
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
उत्तर
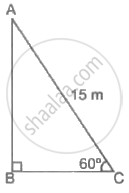
The pole AB in the illustration is where the rope is attached from point C on the ground.
So, AC = 15 m, ∠ACB = 60°
Now, in ΔABC,
`(AB)/(AC)` = sin 60°
`(AB)/15 = sqrt(3)/2`
AB = `(15sqrt(3))/2`
AB = 12.99 m
As a result, the pole's height is 12.99 m.
APPEARS IN
संबंधित प्रश्न
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
In given figure, the value of ZC is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
From the top of building AB, a point C is observed on the ground whose angle of depression is 60° and which is at a distance of 40 m from the base of the building. Complete the following activity to find the height of building AB.

From figure, BC = `square`, ∠ACB = `square`
In ΔACB,
tan `square = square/(BC)`
⇒ `square = square/square`
⇒ `square = square`
Hence, the height of the building AB is `square`.
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.

