Advertisements
Advertisements
प्रश्न
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
विकल्प
\[10\sqrt{3}\]
15 m
\[\frac{30}{\sqrt{3}} m\]
\[15\sqrt{2} m\]
उत्तर
Let h be the height of vertical tower AB
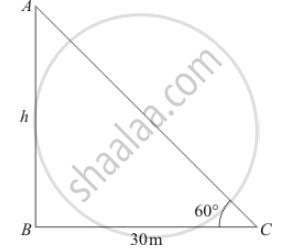
Given that: altitude of sun is 60° and shadow of length `BC=30`meters.
Here, we have to find the height of tower.
So we use trigonometric ratios.
In a triangle ABC,
`⇒ tan C=(AB)/(BC)`
`⇒ tan 60°=(AB)/(BC)`
`⇒sqrt3=h/30`
`⇒h=30sqrt3`
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

In figure given ABCD is a rectangle, the value of CE is ____________.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
