Advertisements
Advertisements
प्रश्न
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
पर्याय
\[10\sqrt{3}\]
15 m
\[\frac{30}{\sqrt{3}} m\]
\[15\sqrt{2} m\]
उत्तर
Let h be the height of vertical tower AB
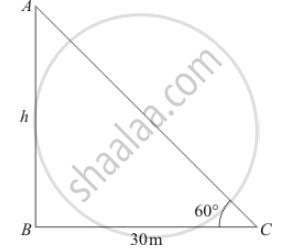
Given that: altitude of sun is 60° and shadow of length `BC=30`meters.
Here, we have to find the height of tower.
So we use trigonometric ratios.
In a triangle ABC,
`⇒ tan C=(AB)/(BC)`
`⇒ tan 60°=(AB)/(BC)`
`⇒sqrt3=h/30`
`⇒h=30sqrt3`
APPEARS IN
संबंधित प्रश्न
A fire in a building B is reported on the telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel?
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
A tower subtends an angle 𝛼 at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tan α cot β
A tower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
Find the distance between the points (a, b) and (−a, −b).
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the distance between the lamp post and the apartment `(sqrt(3) = 1.732)`
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the West of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
