Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
उत्तर
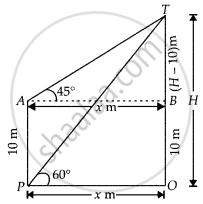
Let the height the vertical tower be
OT = H m and OP = AB = x m
Given that, AP = 10 m
And ∠TPO = 60°, ∠TAB = 45°
Now, in ∆TPO,
tan 60° = `"OT"/"OP" = "H"/x`
⇒ `sqrt(3) = "H"/x`
⇒ `x = "H"/sqrt(3)` ...(i)
And in ∆TAB,
tan 45° = `"TB"/"AB" = ("H" - 10)/x`
⇒ 1 = `("H" - 10)/x`
⇒ `x = "H" - 10`
⇒ `"H"/sqrt(3) = "H" - 10` ...[From equation (i)]
⇒ `"H" - "H"/sqrt(3)` = 10
⇒ `"H"(1 - 1/sqrt(3))` = 10
⇒ `"H"((sqrt(3) - 1)/sqrt(3))` = 10
⇒ H = `(10sqrt(3))/(sqrt(3) - 1)`
∴ H = `(10sqrt(3))/(sqrt(3) - 1) * (sqrt(3) + 1)/(sqrt(3) + 1)` ...[By rationalisation]
= `(10sqrt(3)(sqrt(3) + 1))/(3 - 1)`
= `(10sqrt(3)(sqrt(3) + 1))/2`
⇒ H = `5sqrt(3)(sqrt(3) + 1) = 5(sqrt(3) + 3) "m"`.
Hence, the required height of the tower is `5(sqrt(3) + 3) "m"`.
APPEARS IN
संबंधित प्रश्न
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from her eyes is 45°. What is the height of the tower?
A tower stands vertically on the ground. From a point on the ground, which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]

