Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
उत्तर
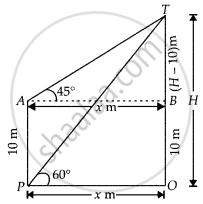
Let the height the vertical tower be
OT = H m and OP = AB = x m
Given that, AP = 10 m
And ∠TPO = 60°, ∠TAB = 45°
Now, in ∆TPO,
tan 60° = `"OT"/"OP" = "H"/x`
⇒ `sqrt(3) = "H"/x`
⇒ `x = "H"/sqrt(3)` ...(i)
And in ∆TAB,
tan 45° = `"TB"/"AB" = ("H" - 10)/x`
⇒ 1 = `("H" - 10)/x`
⇒ `x = "H" - 10`
⇒ `"H"/sqrt(3) = "H" - 10` ...[From equation (i)]
⇒ `"H" - "H"/sqrt(3)` = 10
⇒ `"H"(1 - 1/sqrt(3))` = 10
⇒ `"H"((sqrt(3) - 1)/sqrt(3))` = 10
⇒ H = `(10sqrt(3))/(sqrt(3) - 1)`
∴ H = `(10sqrt(3))/(sqrt(3) - 1) * (sqrt(3) + 1)/(sqrt(3) + 1)` ...[By rationalisation]
= `(10sqrt(3)(sqrt(3) + 1))/(3 - 1)`
= `(10sqrt(3)(sqrt(3) + 1))/2`
⇒ H = `5sqrt(3)(sqrt(3) + 1) = 5(sqrt(3) + 3) "m"`.
Hence, the required height of the tower is `5(sqrt(3) + 3) "m"`.
APPEARS IN
संबंधित प्रश्न
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
