Advertisements
Advertisements
प्रश्न
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
उत्तर
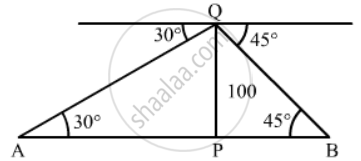
Let PQ be the tower and A and B are two cars.
We have,
PQ = 100 m, ∠PAQ = 30° and ∠PBQ = 45°
In ∆APQ
`tan 30^@ = (PQ)/(AP)`
`=> 1/sqrt3 = 100/(AP)`
`=> AP =100sqrt3` m
Also In ∆ BPQ
`tan 45^@ = (PQ)/(BP)`
`=> 1= 100/(BP)`
`=> BP = 100 m`
Now, AB = AP + BP`
`= 100sqrt3 + 100`
`=100(sqrt3 + 1)`
=100 x (1.732 + 1)
= 100 x 2.732
= 273.2 m
So the distance between the cars is 273.2 m
APPEARS IN
संबंधित प्रश्न
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is:
(A) `4/sqrt3`
(B) `4sqrt3`
(C) `2sqrt2`
(D)4
Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by `\text{cot }\theta =\frac{bcot alpha -a\cot \beta }{b-a}`
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30º. The distance of the car from the tower (in metres) is
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
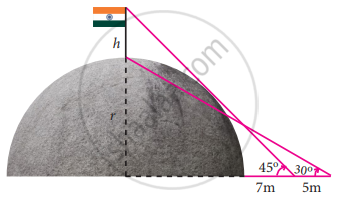
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
