Advertisements
Advertisements
प्रश्न
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
उत्तर
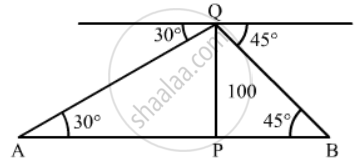
Let PQ be the tower and A and B are two cars.
We have,
PQ = 100 m, ∠PAQ = 30° and ∠PBQ = 45°
In ∆APQ
`tan 30^@ = (PQ)/(AP)`
`=> 1/sqrt3 = 100/(AP)`
`=> AP =100sqrt3` m
Also In ∆ BPQ
`tan 45^@ = (PQ)/(BP)`
`=> 1= 100/(BP)`
`=> BP = 100 m`
Now, AB = AP + BP`
`= 100sqrt3 + 100`
`=100(sqrt3 + 1)`
=100 x (1.732 + 1)
= 100 x 2.732
= 273.2 m
So the distance between the cars is 273.2 m
APPEARS IN
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
In given figure, the value of AE is ____________.
A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
