Advertisements
Advertisements
प्रश्न
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
उत्तर
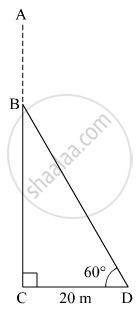
Let AC be the original height of the tree. Suppose BD be the broken part of the tree which is rested at D from the base of the tree.
Here, CD = 20 m and ∠BDC = 60º.
In right ∆BCD,
\[\tan60^\circ = \frac{BC}{CD}\]
\[ \Rightarrow \sqrt{3} = \frac{BC}{20}\]
\[ \Rightarrow BC = 20\sqrt{3} m . . . . . \left( 1 \right)\]
Also,
\[\cos60^\circ = \frac{CD}{BD}\]
\[ \Rightarrow \frac{1}{2} = \frac{20}{BD}\]
\[ \Rightarrow BD = 40 m . . . . . \left( 2 \right)\]
∴ Height of the tree = AB + BC = BD + BC =
\[\left( 40 + 20\sqrt{3} \right) m\] [Using (1) and (2)]
Thus, the height of the tree is \[\left( 40 + 20\sqrt{3} \right) m\]
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [use √3=1.73]
The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the building (use `sqrt3`=1.73)
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
The banks of a river are parallel. A swimmer starts from a point on one of the banks and swims in a straight line inclined to the bank at 45º and reaches the opposite bank at a point 20 m from the point opposite to the starting point. Find the breadth of the river
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
