Advertisements
Advertisements
प्रश्न
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
उत्तर
Let h be the height of aeroplane p above the road.
And A and B be the two consecutive milestones, then AB = 1 mile. we have ∠PAQ = α and ∠PBQ = β.
We have to prove
`h = (tan alpha tan beta)/(tan alpha + tan beta)`
The corresponding figure is as follows
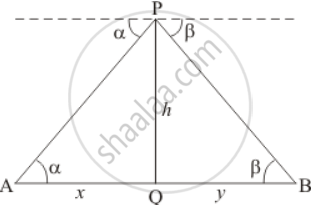
In ΔPAQ
`=> tan alpha = (PQ)/(AQ)`
`=> tan alpha = h/x`
`=> x = h/(tan alpha)`
`=> x = h cot alpha`
Again in ΔPBQ
`=> tan beta =(PQ)/(BQ)`
`=> tan beta = h/y`
`=> y = h/(tan beta)`
`=> y = h cot beta`
Now,
`=> AB = x + y`
`=> AB = h(cot alpha + cot beta)`
`=> AB = h(1/tan alpha + 1/tan beta)`
`=> AB = h((tan alpha + tan beta)/(tan alpha tan beta))`
Therefore `h = (tan alpha tan beta)/(tan alpha + tan beta)` (Since A B = 1)
Hence height of aero plane is `(tan alpha tan beta)/(tan alpha + tan beta)`
APPEARS IN
संबंधित प्रश्न
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
