Advertisements
Advertisements
प्रश्न
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
उत्तर
Let AB be the tower of height H and PQ is a given post of height a, α and β are angles of elevation of the top of tower AB from P and Q. Let PA = x. PQ = a and BC = h.
The corresponding figure is as follows
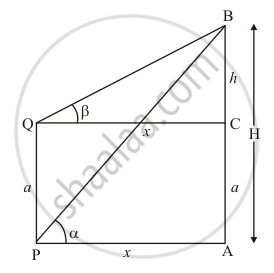
In ΔQCB
`=> tan beta = h/x`
`=> x = h/(tan beta)
Again in ΔPAB
`=> tan alpha = (h + a)/x`
`=> tan alpha = ((h + a)tan beta)/h`
`=> h tan alpha = (h + a)tan beta`
`=> h(tan alpha - tan beta) = a tan beta`
`=> h =(a tan beta)/(tan alpha - tan beta)`
Now
`=> x = (a tan beta)/((tan alpha - tan beta) xx tan beta)`
`=> x = a/(tan alpha - tan beta)`
`=> H = (a tan alpha)/(tan a - tan beta)`
Hence required heigtht is `(a tan alpha)/(tan alpha - tan beta)` And distance is `a/(tan alpha - tan beta)`
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
The Distance of the point (−3, 4) from the x-axis is
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
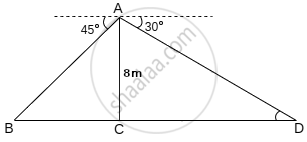
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.