Advertisements
Advertisements
प्रश्न
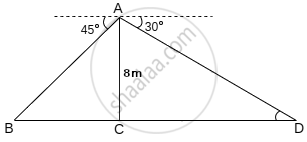
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.
उत्तर
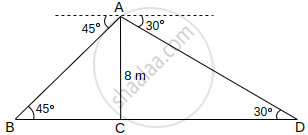
Clearly, ∠ABC = 45° and ∠ADC = 30° ....[∵ Angle of depression = Angle of elevation]
Now, In ΔABC, we have
tan 45° = `("AC")/("BC")`
⇒ 1 = `8/("BC")`
⇒ BC = 8 m ...(i)
Also, In ΔACD, we have
tan 30° = `("AC")/("DC")`
⇒ `1/sqrt(3) = 8/("DC")`
⇒ DC = `8sqrt(3)` ...(ii)
From equations (i) and (ii), we get
BD = BC + DC
= `8 + 8sqrt(3)`
= `8(sqrt(3) + 1)`
= 8(1.732 + 1)
= 8 × 2.732
= 21.856 m
APPEARS IN
संबंधित प्रश्न
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
If a tower 30 m high, casts a shadow `10sqrt3` m long on the ground, then what is the angle of elevation of the sun?
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.
