Advertisements
Advertisements
प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
उत्तर
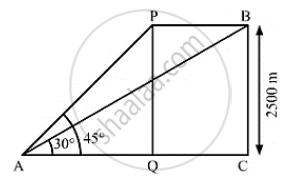
Let the height of flying of the aero-plane be PQ = BC and point A be the point of observation.
We have,
PQ = BC = 2500m, ∠PAQ = 45° and ∠BAC = 30°
In ΔPAQ,
` tan 45° = (PQ)/(AQ)`
`⇒ 1 = 2500/(AQ)`
`⇒AQ = 2500 m`
Also, in ΔABC,
`tan 30° = (BC)/(AC)`
`⇒1/ sqrt(3) = 2500/(AC)`
`⇒ AC = 2500 sqrt(3) m`
Now , QC = AC - AQ
`= 2500 sqrt(3)-2500`
`= 2500( sqrt(3)-1) m`
`= 2500 (1.732 - 1)`
`= 2500(0.732)`
`= 1830 m`
⇒ PB = QC = 1830
So, the speed of the aero-plane`(PB)/15`
`= 1830/15`
=122 m/s
`=122 xx3600/1000 km ⁄ h`
= 439.2 km /5
So, the speed of the aero-plane is 122m/ s or 439.2 km/ h.
APPEARS IN
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
The Distance of the point (−3, 4) from the x-axis is
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
A vertical pole of 30 m is fixed on a tower. From a point on the level ground, the angle of elevation of the top and bottom of the pole is 60° and 45°. Find the height of the tower.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
