Advertisements
Advertisements
प्रश्न
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
उत्तर
MP = YX = 40 m
∴ QM = h - 40
In right angled ΔQMY,
`tan45^@=(QM)/(MY)=>1=(h-40)/(PX) " ...."(MY=PX)`
∴ PX = h - 40 ....(1)
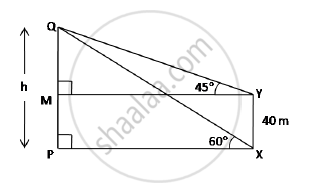
In right angled ΔQPX,
`tan60^@=(QP)/(PX)=>sqrt3=(QP)/(PX)`
∴ `PX=h/sqrt3 " ...(2)"`
From (1) and (2), h - 40 = `h/sqrt3`
`:.sqrt(3h)-40sqrt3=h`
`:.sqrt(3h)-h=40sqrt3`
∴ 1.73h - h=40(1.73) ⇒ h = 94.79 m
Thus, PQ is 94.79 m.
APPEARS IN
संबंधित प्रश्न
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Find the speed of flying of the bird.
`("Take"sqrt3=1.732)`
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, where as for the elder children, she wants to have a steep side at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
In given figure, the value of ZC is ____________.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60°, then the distance between the two towers is ____________.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
