Advertisements
Advertisements
प्रश्न
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, where as for the elder children, she wants to have a steep side at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
उत्तर
It can be observed that AC and PR are the slides for younger and elder children respectively.
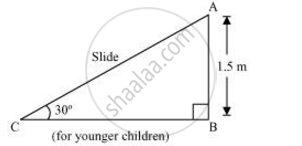
In ΔABC,
`("AB")/("AC")` = sin 30°
`1.5/("AC") = 1/2`
AC = 3 m
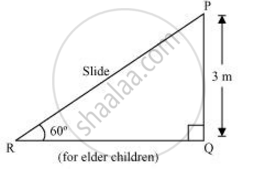
In ΔPQR,
`"PQ"/"PR"` = sin 60°
`3/("PR") = sqrt3/2`
`"PR" = 6/sqrt3`
= `2sqrt3 m`
Therefore, the lengths of these slides are 3 m and `2sqrt3` m.
APPEARS IN
संबंधित प्रश्न
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
A tower subtends an angle 𝛼 at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tan α cot β
A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take `sqrt(3)` =1.732 ]
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60 and 30 respectively. Find the height of the tower and the flagpole mounted on it.
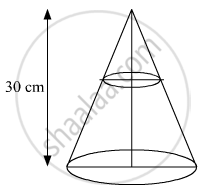
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
The distance of point A(-5, 6) from the origin is ______.
In given figure, the value of CE is ____________.
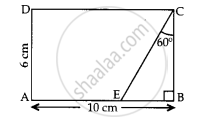
In given figure, the value of ZC is ____________.
A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
