Advertisements
Advertisements
प्रश्न
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
पर्याय
200 m
500 m
30 m
400 m
उत्तर
Let AB be the surface of the lake and P be the point of observation. So AP=60 m.
The given situation can be represented as,
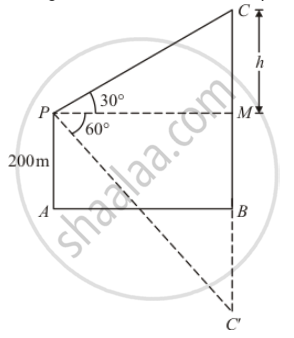
Here,C is the position of the cloud and C' is the reflection in the lake. Then `CB=C'B`.
Let `PM` be the perpendicular from P on CB. Then `∠CPM=30°` and`∠C' PM=60°` and .
Let`CM=h` `PM=x`, , then`CB=h+200` and`C'B=h+200`
Here, we have to find the height of cloud.
So we use trigonometric ratios.
In ,`ΔCMP`
`⇒ tan 30°=CM/PM`
`⇒1/sqrt3=h/x`
`⇒x=sqrt3h`
Again in `ΔPMC`
`⇒ tan 60°= (C'M)/(PM)`
`⇒sqrt3=(C'B+BM)/(PM)`
`⇒sqrt3=(h+200+200)/x`
`⇒ sqrt3x=h+400`
Put `x=sqrt3h`
`⇒3h=h+400`
`⇒ 2h=400`
`⇒h=200`
Now,
`⇒ CB=h+200`
`⇒ CB=200+200`
`⇒ CB=400`
APPEARS IN
संबंधित प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
Find the distance between the points (a, b) and (−a, −b).
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ


