Advertisements
Advertisements
प्रश्न
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
विकल्प
200 m
500 m
30 m
400 m
उत्तर
Let AB be the surface of the lake and P be the point of observation. So AP=60 m.
The given situation can be represented as,
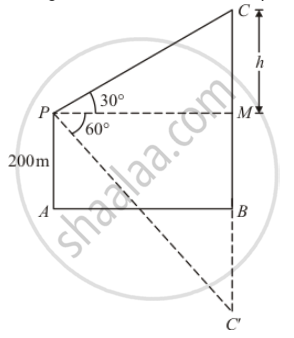
Here,C is the position of the cloud and C' is the reflection in the lake. Then `CB=C'B`.
Let `PM` be the perpendicular from P on CB. Then `∠CPM=30°` and`∠C' PM=60°` and .
Let`CM=h` `PM=x`, , then`CB=h+200` and`C'B=h+200`
Here, we have to find the height of cloud.
So we use trigonometric ratios.
In ,`ΔCMP`
`⇒ tan 30°=CM/PM`
`⇒1/sqrt3=h/x`
`⇒x=sqrt3h`
Again in `ΔPMC`
`⇒ tan 60°= (C'M)/(PM)`
`⇒sqrt3=(C'B+BM)/(PM)`
`⇒sqrt3=(h+200+200)/x`
`⇒ sqrt3x=h+400`
Put `x=sqrt3h`
`⇒3h=h+400`
`⇒ 2h=400`
`⇒h=200`
Now,
`⇒ CB=h+200`
`⇒ CB=200+200`
`⇒ CB=400`
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower. (Use `sqrt3` = 1.73)
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
