Question

The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is

विकल्प

• \[\frac{50}{\sqrt{3 + 1}} m\]

• \[\frac{50}{\sqrt{3 - 1}} m\]

• \[50 \left( \sqrt{3} - 1 \right) m\]

• \[50 \left( \sqrt{3} + 1 \right) m\]

Answer 1

Let AB= h be the light house.

The given situation can be represented as,

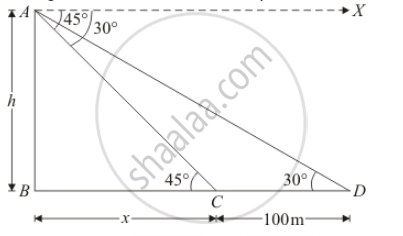
It is clear that`∠C=45°`  and `∠D=30°`

Again, let`BC=x`  and`CD=100` m is given.

Here, we have to find the height of light house.

So we use trigonometric ratios.

In a triangle,`ABC`

`⇒ tan C=AB/BC`

`⇒ tan 45°=h/x`

`⇒ 1=h/x`

`⇒h=x`

Again in a triangle ABD,

`⇒ tan D=(AB)/(BC+CD)`

`⇒ tan 30°= h/(x+100)` 

`⇒1/sqrt3=h/(x+100)`

`⇒sqrt3h=x+100`

Put `x=h`

`⇒ sqrt3h=h+100`

`⇒ h(sqrt3-1)=100`

`⇒h=100/(sqrt3-1)=100`

`⇒ h=100/(sqrt3-1)`

`⇒ h=100/(sqrt3-1) xx (sqrt3+1)/(sqrt3+1)`

`⇒ h=50(sqrt3+1)`