Advertisements
Advertisements
प्रश्न
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
उत्तर
Let AB be the lighthouse of 150 m. and angle of depression of two ship C and D are 30° and 45° respectively.
let BC = x,CD = y and ∠ADB = 30°, ∠ACB = 45°
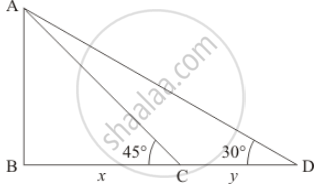
We use trigonometric ratios.
IN a triangle ABC
`=> tan 45^@ = (AB)/(BC)`
`=> 1 = 150/x`
`=> x = 150`
Again in a triangle ABD
`=> tan 30° = (AB)/(BD)`
`=> 1/sqrt3 = 150/(x + y)`
`=> x + y = 150sqrt3`
`=> 150 + y = 150sqrt3`
`=> y = 150sqrt3 - 150`
`=> y = 150(sqrt3 - 1)`
`=> y = 150 xx 0.732`
Hence distance between the ships is 109.8 m
APPEARS IN
संबंधित प्रश्न
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
The angle of elevation of the top of a tower from a point 20 meters away from its base is 45°. The height of the tower is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
A vertical pole of 30 m is fixed on a tower. From a point on the level ground, the angle of elevation of the top and bottom of the pole is 60° and 45°. Find the height of the tower.
