Advertisements
Advertisements
प्रश्न
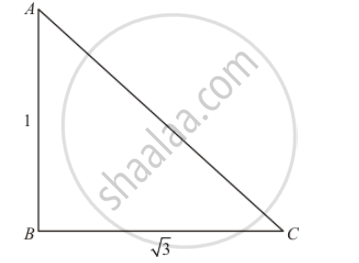
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
विकल्प
30°
45°
60°
90°
उत्तर
Let θ be angle of elevation of sun.
Given that: angle of elevation is `60°`from tower of foot and distance`BC=100` meters.
Here, we have to find the height of tower.
So we use trigonometric ratios.
In a triangle `ABC`
`⇒ tan C=( AB)/(BC)`
`⇒ tan 60°= (AB)/(BC)`
`⇒ sqrt 3=h/100`
`⇒=100sqrt3`
Hence correct option is `a`.
APPEARS IN
संबंधित प्रश्न
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
A kite is flying at a height of 30 m from the ground. The length of string from the kite to the ground is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
