Advertisements
Advertisements
प्रश्न
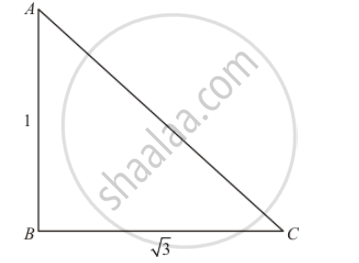
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
पर्याय
30°
45°
60°
90°
उत्तर
Let θ be angle of elevation of sun.
Given that: angle of elevation is `60°`from tower of foot and distance`BC=100` meters.
Here, we have to find the height of tower.
So we use trigonometric ratios.
In a triangle `ABC`
`⇒ tan C=( AB)/(BC)`
`⇒ tan 60°= (AB)/(BC)`
`⇒ sqrt 3=h/100`
`⇒=100sqrt3`
Hence correct option is `a`.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
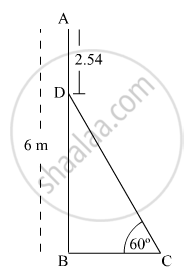
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
Find the distance between the points (a, b) and (−a, −b).
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
