Advertisements
Advertisements
प्रश्न
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
उत्तर
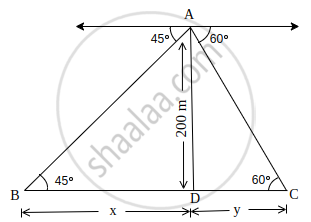
Let the aeroplane's position be A; B and C be two points on the two banks of a river such that the angles of depression at B and C are 45° and 60° respectively.
Let BD = x m, CD = y m
Given, AD = 200 m
In ΔADB, ∠D = 90°
tan 45° = `(AD)/(BD)`
⇒ 1 = `200/x`
⇒ x = 200 m ...(i)
In ΔADC, ∠D = 90°
tan 60° = `(AD)/(CD)`
⇒ `sqrt(3) = 200/y`
⇒ y = `200/sqrt(3)`
⇒ y = `(200sqrt(3))/3` ...(ii)
On adding equations (i) and (ii), we get
x + y = `200 + (200sqrt(3))/3`
= `(600 + 200sqrt(3))/3`
= `(200(3 + sqrt(3)))/3`
= `(200(3 + 1.732))/3`
= `(200 xx 4.732)/3`
= `946.4/3`
= 315.4 m
Hence, the width of the river is 315.4 m.
APPEARS IN
संबंधित प्रश्न
The shadow of a building is 20 m long when the angle of elevation of the sun is 60º. Find the height of the building
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
