Question

From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find

1) the horizontal distance between AB and CD

2) the height of the lamp post.

3) the difference between the heights of the building and the lamp post.

Answer 1

Let AB be the building of height 60 and CD be the lamp post of height h, an angle of depression of the top and bottom of vertical lamp post is 30° and 60° respectively. 

Let AE = h, AC = x, and AC = ED.

it is also given AB = 60 m. Then BE = 60 - h And

∠ACB = 60°, ∠BDE = 30°

We have to find the following

(1) The horizontal distance between AB and CD

(2) The height of lamp post

(3) The difference between the heights of building and the lamp post

We have the corresponding figure as follows

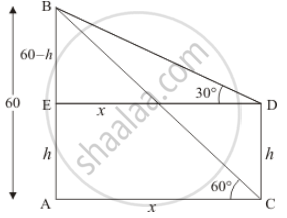
1) So we use trigonometric ratios.

In Δ ABC

`=> tan 60° = (AB)/(AC)`

`=> sqrt3 = 60/x`

`=> x = 60/sqrt3`

`=> x = 34.64`

Hence the distance between AB and CD is 34.64

2) Again in Δ BDE

`=> tan 30^@  = (BE)/(DE)`

`=> 1/sqrt3 = (60 - h)/x`

`=> 60/sqrt3 = (60 - h) sqrt3`

`=> 60 = 180 - 3h`

`=> 3h = 180 - 60`

`=> 3h =  120`

`=> h =  40`

Hence the height of lamp post is 40 m

3) SInce  BE= 60 - h

=> BE = 60 - 40

=> BE = 20

Hence the difference between height of building and lamp post is 20 m

Answer 2

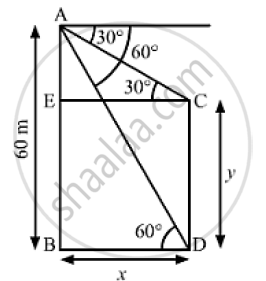
We have,
AB = 60m, ∠ACE = 30° and ∠ADB = 60°
Let BD =CE = x and CD = BE = y
⇒ AE = AB - BE = 60 - y
In ΔACE,

`tan 30° = (AE)/(CE)`

`⇒ 1/ sqrt(3) = (60-y)/x`

`⇒ x = 60 sqrt(3)- y sqrt(3)`                    ............(1)

Also in ,Δ ABD,

`⇒ tan 60° = (AB)/(BD)`

`⇒ sqrt(3) = 60/x`

`⇒ x = 60/ sqrt(3)`

`⇒ x = 60/ sqrt( 3) xx sqrt(3) / sqrt(3)`

`⇒x = (60- sqrt(3))/3`

`⇒ x = 20 sqrt(3)`

Substituting x =20` sqrt(3)` in (i), we get

`20 sqrt(3) = 60 sqrt(3) - ysqrt(3)`

`⇒ y sqrt(3) = 60 sqrt(3) - 20 sqrt(3)`

`⇒y sqrt(3) = 40 sqrt(3) `

`⇒ y = ( 40 sqrt(3))/sqrt(3)`

⇒ y = 40 m

(i) The horizontal distance between AB and CD = BD = x

`= 20 sqrt(3)`

= 20×1.732

=34.64 m

(ii) The height of the lamp post = CD = y = 40m

(iii) the difference between the heights of the building and the lamp post

=AB-CD=60-40=20m