Advertisements
Advertisements
प्रश्न
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
उत्तर १
Let AB be the building of height 60 and CD be the lamp post of height h, an angle of depression of the top and bottom of vertical lamp post is 30° and 60° respectively.
Let AE = h, AC = x, and AC = ED.
it is also given AB = 60 m. Then BE = 60 - h And
∠ACB = 60°, ∠BDE = 30°
We have to find the following
(1) The horizontal distance between AB and CD
(2) The height of lamp post
(3) The difference between the heights of building and the lamp post
We have the corresponding figure as follows
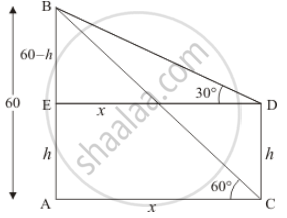
1) So we use trigonometric ratios.
In Δ ABC
`=> tan 60° = (AB)/(AC)`
`=> sqrt3 = 60/x`
`=> x = 60/sqrt3`
`=> x = 34.64`
Hence the distance between AB and CD is 34.64
2) Again in Δ BDE
`=> tan 30^@ = (BE)/(DE)`
`=> 1/sqrt3 = (60 - h)/x`
`=> 60/sqrt3 = (60 - h) sqrt3`
`=> 60 = 180 - 3h`
`=> 3h = 180 - 60`
`=> 3h = 120`
`=> h = 40`
Hence the height of lamp post is 40 m
3) SInce BE= 60 - h
=> BE = 60 - 40
=> BE = 20
Hence the difference between height of building and lamp post is 20 m
उत्तर २
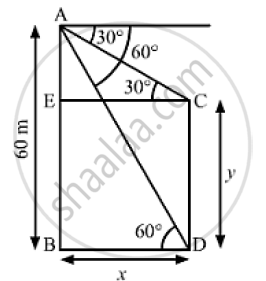
We have,
AB = 60m, ∠ACE = 30° and ∠ADB = 60°
Let BD =CE = x and CD = BE = y
⇒ AE = AB - BE = 60 - y
In ΔACE,
`tan 30° = (AE)/(CE)`
`⇒ 1/ sqrt(3) = (60-y)/x`
`⇒ x = 60 sqrt(3)- y sqrt(3)` ............(1)
Also in ,Δ ABD,
`⇒ tan 60° = (AB)/(BD)`
`⇒ sqrt(3) = 60/x`
`⇒ x = 60/ sqrt(3)`
`⇒ x = 60/ sqrt( 3) xx sqrt(3) / sqrt(3)`
`⇒x = (60- sqrt(3))/3`
`⇒ x = 20 sqrt(3)`
Substituting x =20` sqrt(3)` in (i), we get
`20 sqrt(3) = 60 sqrt(3) - ysqrt(3)`
`⇒ y sqrt(3) = 60 sqrt(3) - 20 sqrt(3)`
`⇒y sqrt(3) = 40 sqrt(3) `
`⇒ y = ( 40 sqrt(3))/sqrt(3)`
⇒ y = 40 m
(i) The horizontal distance between AB and CD = BD = x
`= 20 sqrt(3)`
= 20×1.732
=34.64 m
(ii) The height of the lamp post = CD = y = 40m
(iii) the difference between the heights of the building and the lamp post
=AB-CD=60-40=20m
संबंधित प्रश्न
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, where as for the elder children, she wants to have a steep side at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
