Advertisements
Advertisements
प्रश्न
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
उत्तर
Let AB be the flag of length hm on the building BC.
We assume that BC = 10, ∠APC = 45°, ∠BPC = 30°
Now we have to find height of flag-staff and distance of the point P from the building
The corresponding figure is as follows
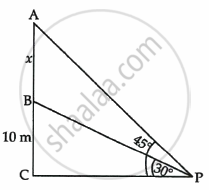
In a triangle BPC,
`=> tan "P" = ("BC")/("CP")`
`=> tan 30^@ = ("BC")/("CP")`
`=> "CP"="BC"/tan30^@`
`=> 10/(1/sqrt3)`
`= 10sqrt3` m
Again in a triangle ACP
`=> tan "P" = ("AC")/"CP"`
`=> 1 = ("AC")/"CP"`
`=>` AC = CP = 10`sqrt3` m
`=>` AB + BC = CP
`=>` x = 10 = 10`sqrt3`
`=> x = 10sqrt3-10`
`=>10(sqrt3-1)`
= 10 × 0.73
h = 7.32
Hence the length is 17.32 m and distance is 7.32 m
APPEARS IN
संबंधित प्रश्न
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
A passenger, while boarding the plane, slipped form the stairs and got hurt. The pilot took the passenger in the emergency clinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/hour than the usual speed. Find the usual speed of the plane
What value is depicted in this question?
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ


