Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
विकल्प
\[\frac{d}{cot \alpha + cot \beta}\]
\[\frac{d}{cot \alpha + cot \beta}\]
\[\frac{d}{\tan \beta - \tan \alpha}\]
\[\frac{d}{\tan \beta - \tan \alpha}\]
उत्तर
The given information can be represented with the help of a diagram as below.
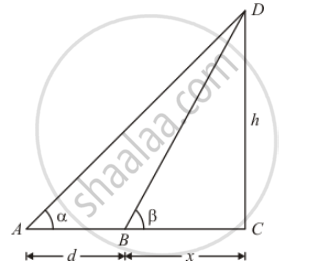
Here, CD = h is the height of the tower. Length of BC is taken as x.
In`Δ ACD`
`tan A=(CD)/(AC)`
`tan∝=h/(d+x)`
`h=(d+x)tan∝ `............(1)
In ΔBCD.
`tan ß = CD/BC`
`tan ß=h/x`
`x=h cot ß` ...............(2)
From (1) and (2)
`h=(d+h cot ß)tan ∝`
`h=d tan ∝+h cot ß tan ∝`
`h(1-cot ß tan ∝ )= d tan ∝`
`h=d tan ∝/((1-cot ß tan ∝ ))=d/(cot ∝-cot ß)`
APPEARS IN
संबंधित प्रश्न
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
