Advertisements
Advertisements
Question
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
Options
\[\frac{d}{cot \alpha + cot \beta}\]
\[\frac{d}{cot \alpha + cot \beta}\]
\[\frac{d}{\tan \beta - \tan \alpha}\]
\[\frac{d}{\tan \beta - \tan \alpha}\]
Solution
The given information can be represented with the help of a diagram as below.
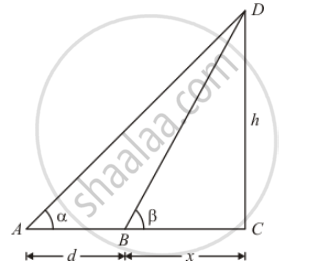
Here, CD = h is the height of the tower. Length of BC is taken as x.
In`Δ ACD`
`tan A=(CD)/(AC)`
`tan∝=h/(d+x)`
`h=(d+x)tan∝ `............(1)
In ΔBCD.
`tan ß = CD/BC`
`tan ß=h/x`
`x=h cot ß` ...............(2)
From (1) and (2)
`h=(d+h cot ß)tan ∝`
`h=d tan ∝+h cot ß tan ∝`
`h(1-cot ß tan ∝ )= d tan ∝`
`h=d tan ∝/((1-cot ß tan ∝ ))=d/(cot ∝-cot ß)`
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
From a point P on the ground the angle of elevation of the top of a tower is 30° and that of the top of a flag staff fixed on the top of the tower, is 60°. If the length of the flag staff is 5 m, find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
