Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
पर्याय
\[\frac{d}{cot \alpha + cot \beta}\]
\[\frac{d}{cot \alpha + cot \beta}\]
\[\frac{d}{\tan \beta - \tan \alpha}\]
\[\frac{d}{\tan \beta - \tan \alpha}\]
उत्तर
The given information can be represented with the help of a diagram as below.
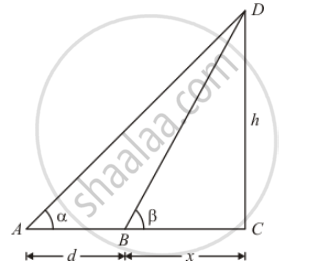
Here, CD = h is the height of the tower. Length of BC is taken as x.
In`Δ ACD`
`tan A=(CD)/(AC)`
`tan∝=h/(d+x)`
`h=(d+x)tan∝ `............(1)
In ΔBCD.
`tan ß = CD/BC`
`tan ß=h/x`
`x=h cot ß` ...............(2)
From (1) and (2)
`h=(d+h cot ß)tan ∝`
`h=d tan ∝+h cot ß tan ∝`
`h(1-cot ß tan ∝ )= d tan ∝`
`h=d tan ∝/((1-cot ß tan ∝ ))=d/(cot ∝-cot ß)`
APPEARS IN
संबंधित प्रश्न
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is
`\frac{h(\tan\alpha +\tan \beta )}{\tan \beta -\tan \alpha }`
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
