Advertisements
Advertisements
प्रश्न
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
उत्तर
An aeroplane is flying 1 km above the ground making an angle of elevation of aeroplane 60°. After 10 seconds angle of elevation is changed to 30°.
Let CE = x, BC = y, ∠AEB = 30°, ∠DEC = 60°, AB = 1 km and CD = 1 km.
Here we have to find the speed of an aeroplane.
The corresponding figure is as follows
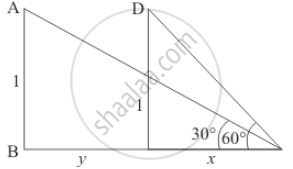
So we use trigonometric ratios.
In ΔDCE
`=> tan 60^@ = 1/x`
`=> sqrt3 = 1/x`
`=> x = 1/sqrt3`
Again in Δ ABE
`=> tan 30^@ = 1/(x + y)`
`=> 1/sqrt3 = 1/(x + y)`
`=> x + y = sqrt3`
`=> y = sqrt3 - 1/sqrt3`
`=> y = 2/sqrt3``
speed = "distance"/"time"`
`= y/(10 sec)`
`= (2/sqrt3)/(10/(60 xx 60))`
= 415.68
Hence the speed of aeroplace is 415.68 km/h.
APPEARS IN
संबंधित प्रश्न
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
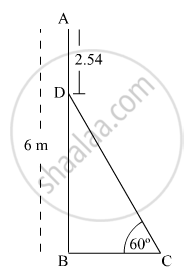
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
An electrician has to repair an electric fault on a pole of height 4 meters. He needs to reach a point 1 meter below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the West of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
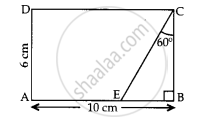
In given figure, the value of CE is ____________.
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
