Advertisements
Advertisements
प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
उत्तर
Let angle of elevation of an aeroplane is 45°. After 15 seconds angle of elevation is the change to 30°. Let DE be the height of aeroplane which is 3000 meters above the ground.
Let AB = x,BD = y, ∠CAB = 45° and ∠EAD = 30°
Here we have to find speed of aero plane.
We have the corresponding figure as follows
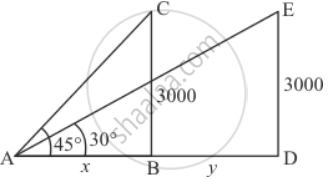
So we use trigonometric ratios.
In Δ ABC
`=> tan A = (BC)/(AB)`
`=> tan 45^@ = 3000/x`
`=> 1 = 3000/x`
`=> x = 3000`
Again in ΔADE
`=> tan A = (DE)/(AB + BD)`
`=> tan 30^@ = 3000/(x + y)`
`=> 1/sqrt3 = 3000/(3000 + y)`
`=> 3000 + y = 3000sqrt3`
`=> y = 3000sqrt3 - 3000`
`=> y = 3000(sqrt3 - 1)`
=> y = 2196
Since 15 sec = 2196
`=> sec = 2196/15 = 146.4`
`= (146.4 xx 3600)/1000`
= 527.04
Hence the speed of aero plane is 527.04 km/h
APPEARS IN
संबंधित प्रश्न
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the North of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
In given figure, the value of CE is ____________.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.
