Question

A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.

Answer 1

Let the height of the other house = OQ = Hm and OB = MW = xm

Given, height of the first house = WB = h = MO

And ∠QWM = α, ∠OWM = β = ∠WOB   ...[Alternate angle]

Now, ∆WOB,

tan β = `"WB"/"OB" = "h"/x`

⇒ x = `"h"/(tan β)`  ...(i)

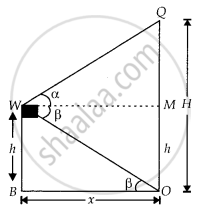
And in ΔQWM,

tan α = `"QM"/"WM"`

= `("OQ" - "MO")/"WM"`

⇒ tan α = `("H" - "h")/x`

⇒ x = `("H" - "h")/(tan α)`   ...(ii)

From equations (i) and (ii), we get

`"h"/(tan β) = ("H" - "h")/(tan α)`

⇒ h tan α = (H – h)tan β

⇒ h tan α = H tan β – h tan β

⇒ H tan β = h(tan α + tan β)

⇒ H = `"h"((tan α + tan β)/ tan β)`

⇒ H = `"h"(1 + tan α * 1/tan β)`  ...`[∵ cot θ = 1/tan θ]`

= h(1 + tan α · cot β)

Hence, the required height of the other house is h(1 + tanα · cotβ)