Advertisements
Advertisements
Question
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
Solution
Let the height of the other house = OQ = Hm and OB = MW = xm
Given, height of the first house = WB = h = MO
And ∠QWM = α, ∠OWM = β = ∠WOB ...[Alternate angle]
Now, ∆WOB,
tan β = `"WB"/"OB" = "h"/x`
⇒ x = `"h"/(tan β)` ...(i)
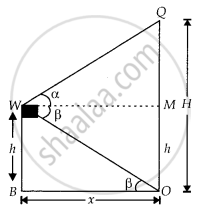
And in ΔQWM,
tan α = `"QM"/"WM"`
= `("OQ" - "MO")/"WM"`
⇒ tan α = `("H" - "h")/x`
⇒ x = `("H" - "h")/(tan α)` ...(ii)
From equations (i) and (ii), we get
`"h"/(tan β) = ("H" - "h")/(tan α)`
⇒ h tan α = (H – h)tan β
⇒ h tan α = H tan β – h tan β
⇒ H tan β = h(tan α + tan β)
⇒ H = `"h"((tan α + tan β)/ tan β)`
⇒ H = `"h"(1 + tan α * 1/tan β)` ...`[∵ cot θ = 1/tan θ]`
= h(1 + tan α · cot β)
Hence, the required height of the other house is h(1 + tanα · cotβ)
APPEARS IN
RELATED QUESTIONS
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Find the speed of flying of the bird.
`("Take"sqrt3=1.732)`
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
The angle of elevation of the top of a tower from a point 20 meters away from its base is 45°. The height of the tower is ____________.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
Lakshaman Jhula is located 5 kilometers north-east of the city of Rishikesh in the Indian state of Uttarakhand. The bridge connects the villages of Tapovan to Jonk. Tapovan is in Tehri Garhwal district, on the west bank of the river, while Jonk is in Pauri Garhwal district, on the east bank. Lakshman Jhula is a pedestrian bridge also used by motorbikes. It is a landmark of Rishikesh. A group of Class X students visited Rishikesh in Uttarakhand on a trip. They observed from a point (P) on a river bridge that the angles of depression of opposite banks of the river are 60° and 30° respectively. The height of the bridge is about 18 meters from the river. |
Based on the above information answer the following questions.
- Find the distance PA.
- Find the distance PB
- Find the width AB of the river.
[OR]
Find the height BQ if the angle of the elevation from P to Q be 30°.
