Advertisements
Advertisements
प्रश्न
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
उत्तर
Let the height of the other house = OQ = Hm and OB = MW = xm
Given, height of the first house = WB = h = MO
And ∠QWM = α, ∠OWM = β = ∠WOB ...[Alternate angle]
Now, ∆WOB,
tan β = `"WB"/"OB" = "h"/x`
⇒ x = `"h"/(tan β)` ...(i)
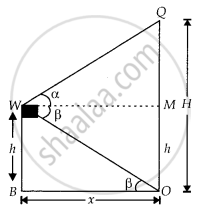
And in ΔQWM,
tan α = `"QM"/"WM"`
= `("OQ" - "MO")/"WM"`
⇒ tan α = `("H" - "h")/x`
⇒ x = `("H" - "h")/(tan α)` ...(ii)
From equations (i) and (ii), we get
`"h"/(tan β) = ("H" - "h")/(tan α)`
⇒ h tan α = (H – h)tan β
⇒ h tan α = H tan β – h tan β
⇒ H tan β = h(tan α + tan β)
⇒ H = `"h"((tan α + tan β)/ tan β)`
⇒ H = `"h"(1 + tan α * 1/tan β)` ...`[∵ cot θ = 1/tan θ]`
= h(1 + tan α · cot β)
Hence, the required height of the other house is h(1 + tanα · cotβ)
संबंधित प्रश्न
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
An observer , 1.7 m tall , is` 20 sqrt3` m away from a tower . The angle of elevation from the eye of an observer to the top of tower is 300 . Find the height of the tower.
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

