Question

The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.

Answer 1

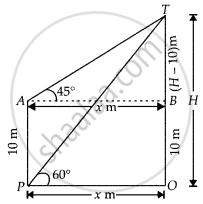
Let the height the vertical tower be

OT = H m and OP = AB = x m

Given that, AP = 10 m

And ∠TPO = 60°, ∠TAB = 45°

Now, in ∆TPO,

tan 60° = ${\displaystyle \frac{\text{OT}}{\text{OP}}=\frac{\text{H}}{x}}$

⇒ ${\displaystyle \sqrt{3}=\frac{\text{H}}{x}}$

⇒ ${\displaystyle x=\frac{\text{H}}{\sqrt{3}}}$  ...(i)

And in ∆TAB,

tan 45° =  ${\displaystyle \frac{\text{TB}}{\text{AB}}=\frac{\text{H}-10}{x}}$

⇒ 1 = ${\displaystyle \frac{\text{H}-10}{x}}$

⇒ ${\displaystyle x=\text{H}-10}$

⇒ ${\displaystyle \frac{\text{H}}{\sqrt{3}}=\text{H}-10}$  ...[From equation (i)]

⇒ ${\displaystyle \text{H}-\frac{\text{H}}{\sqrt{3}}}$ = 10

⇒ ${\displaystyle \text{H}(1-\frac{1}{\sqrt{3}})}$ = 10

⇒ ${\displaystyle \text{H}\left(\frac{\sqrt{3}-1}{\sqrt{3}}\right)}$ = 10

⇒ H = ${\displaystyle \frac{10\sqrt{3}}{\sqrt{3}-1}}$

∴ H = ${\displaystyle \frac{10\sqrt{3}}{\sqrt{3}-1}\cdot \frac{\sqrt{3}+1}{\sqrt{3}+1}}$  ...[By rationalisation]

= ${\displaystyle \frac{10\sqrt{3}(\sqrt{3}+1)}{3-1}}$

= ${\displaystyle \frac{10\sqrt{3}(\sqrt{3}+1)}{2}}$

⇒ H = ${\displaystyle 5\sqrt{3}(\sqrt{3}+1)=5(\sqrt{3}+3)\text{m}}$.

Hence, the required height of the tower is ${\displaystyle 5(\sqrt{3}+3)\text{m}}$.