Question

A ladder rests against a vertical wall at an inclination α to the horizontal. Its foot is pulled away from the wall through a distance p so that its upper end slides a distance q down the wall and then the ladder makes an angle β to the horizontal. Show that `p/q = (cos β - cos α)/(sin α - sin β)`

Answer 1

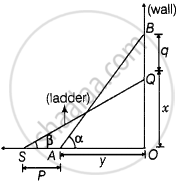
Let OQ = x and OA = y

Given that, BQ = q, SA = P and AB = SQ = Length of ladder

Also, ∠BAO = α and ∠QSO = β

Now, In ΔBAO,

cos α = `"OA"/"AB"`

⇒ cos α = `y/"AB"`

⇒ y = AB cos α = OA  ...(i)

And sin α = `"OB"/"AB"`

⇒ OB = BA sin α   ...(ii)

Now, In ΔQSO

cos β = `"OS"/"SQ"`

⇒ OS = SQ cos β = AB cos β  ...[∵ AB = SQ]  ...(iii)

And sin β = `"OQ"/"SQ"`

⇒ OQ = SQ sin β = AB sin β  ...[∵ AB = SQ]  ...(iv)

Now, SA = OS – AO

P = AB cos β – AB cos α

⇒ P = AB(cos β – cos α)  ...(v)

And BQ = BO – QO

⇒ q = BA sin α – AB sin β

⇒ q = AB(sin α – sin β)  ...(vi)

Equation (v) divided by Equation (vii), we get

`"p"/"q" = ("AB"(cos β - cos α))/("AB"(sin α - sin β)) = (cos β - cos α)/(sin α - sin β)`

⇒ `"p"/"q" = (cos β - cos α)/(sin α - sin β)`

Hence proved.