Advertisements
Advertisements
Question
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
Solution
Given: the height of tower is h m.
∠ABD = α and ∠ACD = β
Let CD = y and BC = x

In ∆ABD,
tan α = `"AD"/"BD"`
⇒ tan α = `"h"/("BC" + "CD")`
⇒ tan α = `"h"/(x + y)`
⇒ x + y = `"h"/tan α`
⇒ y = `"h"/tan α - x` ...[Equation 1]
In ∆ACD,
tan β = `"AD"/"CD"`
⇒ tan β = `"h"/y`
⇒ y = `"h"/tan β` ...[Equation 2]
Comparing equation 1 and equation 2,
`"h"/tan α - x = "h"/tan β`
⇒ x = `"h"/tan α - "h"/tan β`
⇒ x = `"h"(1/tan α - 1/tan β)`
⇒ x = h(cot α – cot β)
Hence, we have got the required distance between the two points, i.e. h(cot α – cot β)
APPEARS IN
RELATED QUESTIONS
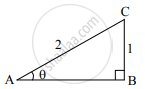
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
