Advertisements
Advertisements
Question
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
Solution
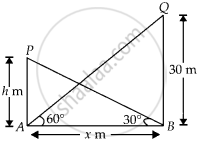
Let distance between the two towers = AB = x m
And height of the other tower = PA = h m
Given, height of the tower = QB = 30 m, ∠QAB = 60° and ∠PBA = 30°
Now, in ∆QAB,
tan 60° = `"QB"/"AB" = 30/x`
⇒ `sqrt(3) = 30/x`
⇒ `x = 30/sqrt(3)`
⇒ `x = 30/sqrt(3) * sqrt(3)/sqrt(3)`
= `(30sqrt(3))/3`
= `10sqrt(3)`
And in ∆PBA,
tan 30° = `"PA"/"AB" = "h"/x`
⇒ `1/sqrt(3) = "h"/(10sqrt(3))` ...`[∵ x = 10sqrt(3) "m"]`
⇒ h = 10
Hence, the required distance and height are `10sqrt(3) "m"` and 10 m, respectively.
APPEARS IN
RELATED QUESTIONS
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is 30° and the angle of depression of its shadow in water of lake is 60°. Find the height of the cloud from the surface of water
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
The distance of point A(-5, 6) from the origin is ______.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
