Advertisements
Advertisements
Question
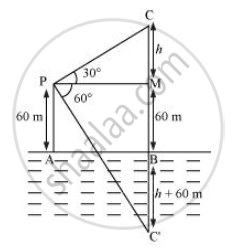
The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is 30° and the angle of depression of its shadow in water of lake is 60°. Find the height of the cloud from the surface of water
Solution
Let AB be the surface of the lake and P be the point of observation such that AP = 60 m. Let C be the position of the cloud and C be its reflection in the lake
Then CB = C'B
Draw PM⊥CB
Let CM = h
∴ CB = h + 60 m

From equations (1) and (2):
`sqrt3h = (h + 120m)/sqrt3`
⇒ 3h = h + 120 m
⇒ 2h = 120 m
⇒ h = 60 m
CB = h + 60m = 60m + 60m = 120m
Thus, the height of the cloud from the surface of the lake is 120 m
APPEARS IN
RELATED QUESTIONS
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
In figure given ABCD is a rectangle, the value of CE is ____________.

The line drawn from the eye of an observer to the point in the object viewed by the observer is known as ____________.
