Advertisements
Advertisements
Question
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
Solution
Let A and B the position of the first ship and the second ship
Distance = `200((sqrt(3) + 1)/sqrt(3))`m
Let the height of the lighthouse CD be h
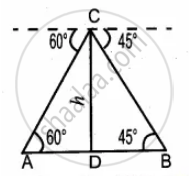
In the right ∆ACD, tan 60° = `"CD"/"AD"`
`sqrt(3) = "h"/"AD"`
∴ AD = `"h"/sqrt(3` ...(1)
In the right ∆BCD
tan 45° = `"DC"/"BD"`
1 = `"h"/"BD"`
∴ BD = h
Distance between the two ships = AD + BD
`200((sqrt(3) + 1)/sqrt3) = "h"/sqrt3 + "h"`
⇒ `200 (sqrt(3) + 1) = "h" + sqrt(3)"h"`
`200(sqrt(3) + 1) = "h"(1 + sqrt(3))`
⇒ h = `(200(sqrt(3) + 1))/((1 + sqrt(3))`
h = 200
Height of the light house = 200 m
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing. (sin 20° = 0.342)
The length of shadow of a tower on the plane ground is \[\sqrt{3}\] times the height of the tower. The angle of elevation of sun is
