Advertisements
Advertisements
Question
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
Solution
Let AC be the pedestal and BC be the statue such that BC = 1.46m.
We have:
∠ADC = 45° and ∠ADB = 60°
Let:
AC = hm and AD = xm
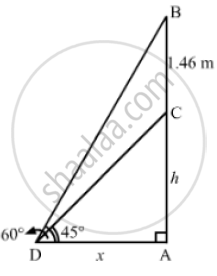
In the right ΔADC,we have:
`(AC)/(AD) = tan 45° = 1`
`⇒ h/x = 1`
⇒ h = x
Or,
x = h
Now, in the right ΔADB,we have:
`(AB)/(AD) = tan 60° = sqrt(3)`
`(h+1.46)/x = sqrt(3)`
On putting x = h in the above equation, we get
`(h+1.46)/h = sqrt(3)`
`⇒ h + 1.46 = sqrt(3)h`
`⇒ h( sqrt(3)-1) = 1.46`
`⇒ h = 1.46/( sqrt(3)-1) = 1.46/0.73 = 2m`
Hence, the height of the pedestal is 2 m.
APPEARS IN
RELATED QUESTIONS
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
Two men on either side of a 75 m high building and in line with base of building observe the angles of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use\[\sqrt{3} = 1 . 73\])
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
In given figure, the length of AP is ____________.

In figure given ABCD is a rectangle, the value of CE is ____________.

Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
