Advertisements
Advertisements
Question
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
Solution
An aeroplane is flying 1 km above the ground making an angle of elevation of aeroplane 60°. After 10 seconds angle of elevation is changed to 30°.
Let CE = x, BC = y, ∠AEB = 30°, ∠DEC = 60°, AB = 1 km and CD = 1 km.
Here we have to find the speed of an aeroplane.
The corresponding figure is as follows
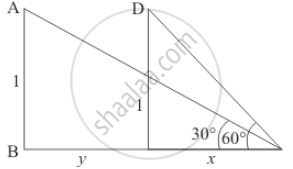
So we use trigonometric ratios.
In ΔDCE
`=> tan 60^@ = 1/x`
`=> sqrt3 = 1/x`
`=> x = 1/sqrt3`
Again in Δ ABE
`=> tan 30^@ = 1/(x + y)`
`=> 1/sqrt3 = 1/(x + y)`
`=> x + y = sqrt3`
`=> y = sqrt3 - 1/sqrt3`
`=> y = 2/sqrt3``
speed = "distance"/"time"`
`= y/(10 sec)`
`= (2/sqrt3)/(10/(60 xx 60))`
= 415.68
Hence the speed of aeroplace is 415.68 km/h.
APPEARS IN
RELATED QUESTIONS
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
In given figure, ABCD is a || gm. The length of AP is ____________.
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
