Advertisements
Advertisements
Question
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
Solution
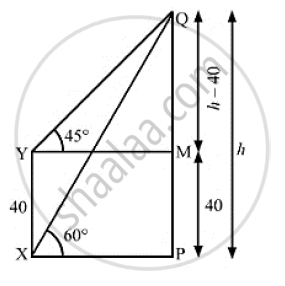
We have
XY = 40m,∠PXQ = 60° and ∠MYQ = 45°
Let PQ = h
Also, MP = XY = 40m, MQ = PQ - MP = h - 40
In ΔMYQ,
` tan 45° = (MQ)/(MY)`
`⇒1 = (h-40)/(MY)`
⇒ MY = H - 40
⇒ PX = MY = h - 40 ................(1)
Now , in ΔMXQ,
`tan 60° = (PQ)/(PX)`
`⇒ sqrt(3) = h/( h-40)` [From (i)]
`⇒ h sqrt(3) - 40 sqrt(3) = h `
`⇒ h sqrt(3) -h = 40 sqrt(3)`
`⇒ h (sqrt(3)-1) = 40 sqrt(3)`
`⇒ h = (40sqrt(3))/((sqrt(3)-1))`
`⇒ h = (40 sqrt(3))/((sqrt (3)-1)) xx ((sqrt(3)+1))/((sqrt(3)+1))`
`⇒ h = (40 sqrt(3)(sqrt(3)+1))/((3-1))`
`⇒h = (40 sqrt(3) ( sqrt(3) +1))/2`
`⇒h= 20sqrt(3) (sqrt(3)+1)`
`⇒ h= 60+20 sqrt(3)`
`⇒ h= 60+20xx 1.73`
`⇒h = 60+ 34.6`
∴ h = 94.6m
So, the height of the tower PQ is 94. 6 m.
APPEARS IN
RELATED QUESTIONS
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
